LOGIKA INFORMATIKA

A. HIMPUNAN
Himpunan matematika dapat didefinisikan sebagai sebuah kumpulan dari beberapa objek baik itu benda abstrak maupun benda real (nyata) yang dapat didefinisikan dengan jelas. Artinya benda-benda tersebut jelas adanya dan memiliki keterangan yang jelas.
a. Sifat-Sifat Himpunan
1. Komutatif
a. Irisan
Berlaku bila A B = B A
b. Gabungan
Berlaku bila A B = B A
2. Asosiatif
a. Irisan tiga himpunan yaitu (A B) C = A ( B C)
b. Gabungan tiga himpunan yaitu (A B) C = A ( B C)
3. Distributif
a. Gabungan yaitu A (B C) = (A B) (A C)
b. Irisan yaitu A ( B C ) = (A B) (A C)
a. Macam-macam  HIMPUNAN 
1.Himpunan berhingga adalah suatu himpunan yang jumlah anggotanya dapat dihitung. 
Contohnya D = {bilangan genap kurang dari 10} atau A = {2,4,6,8}. 
Himpunan D jumlah angotanya dapat dihitung yaitu sebanyak 4 buah. 
2. Himpunan tak hingga adalah suatu himpunan yang jumlah anggotanya tidak terbatas atau tak hingga. Contohnya: A= {bilangan genap}, B= {bilangan ganjil} 
3.Himpunan kosong adalah suatu himpunan yang tidak memiliki anggota sama sekali. Himpunan kosong dilambangkan dengan tanda {}. 
Contohnya B = {bilangan genap antara 2 dan 4}. ditulis B={}={0}.
4.Himpunan ekuivalen/himpunan sama adalah himpunan yang anggotanya sama
   contohnya A= {b,c,d} B={d,c,b} A=B
5.Himpunan semesta adalah himpunan dari semua unsur yang sedang dibicarakan. Himpunan semesta juga disebut himpunan uiversal dan ditulis dengan huruf S.
contohnya:A = {1,3,5,7,9}
himpunan semestanya berupa:
S = {bilangan asli}
S = {bilangan cacah} 
S = {bilangan ganjil kurang dari 10}
6.Himpunan bilangan cacah adalah himpunan bilangan yang anggotanya dimulai dari nol dan seterusnya contoh K = {0,1,2,3,4,5}  
7.Himpunan bagian adalah apabila setiap unsur dalam himpunan B termasuk juga anggota A, maka B merupakan bagian dari himpunan A. contohnya B = {a,c,e} A = {a,b,c,d,e} 
jadi B bagian dari A.Anggota himpunan n adalah suatu unsur dari suatu himpunan.Contohnya : A = (a,b,c,d,e} maka a elemen A
8.Himpunan lepas adalah ssuatu himpunan yang tidak mempunyai anggota persekutuan dengan himpunan lain. ContohnyaA = {d,e,f} B = {g,h,i} maka himpunan A tidak mempunyai anggota persekutuan dengan himpunan B atau A//B bukan anggota himpunan adalah unsur ini tidak termasuk dalam himpunan tersebutcontohnya A = {a,b,c,d} e bukan anggota himpunan A.
9.Himpunan bilangan asli adalah himpunan bilangan yang anggotanya dimulai dari bilangan satu dan seterusnya.Contohnya D = {1,2,3,4,...}
10. Himpunan bilangan genap adalah himpunan yang anggotanya dimulai dari angka dua dan selalu genap atau habis dibagi dua contohnya G = {2,4,6,8,10}
11.Himpunan bilangan ganjil adalah himpunan yang anggota bilanganya tidak habis dibagi dua .contohnya K = {1,3,5,7}  
12.Himpunan bilangan prima adalah himpunan bilangan yang anggotanya semua bilangan yang memiliki dua faktor contohnya Y = {2,3,,5,7} 
13. Himpunan kuadrat bilangan cacah adalah himpunan bilangan cacah yang anggotanya dipangkatkan dua.Contohnya Y = {0^2,1^2,3^2)
b. RELASI ANTAR HIMPUNAN

Relasi, dalam matematika adalah hubungan antara dua elemen himpunan. Hubungan ini bersifat abstrak, dan tidak perlu memiliki arti apapun baik secara konkrit maupun secara matematis.

Relasi antara dua himpunan adalah Suatu pemasangan anggota-anggota A dengan anggota-anggota B. 

Kita dapat membuat relasi antara anggota himpunan A dan himpunan B dari

kehidupan sehari-hari yang kita temukan. Contoh relasiseperti : "anak dari",

"gemar berolahraga","ibu kota dari", dsb.

   Contoh :

Cecep sedang berulang tahun yang ke-15. Ia mengajak teman-temannya: Aris, Bari, Fira dan Darla pergi ke rumah makan “Aneka Sari”. Perhatikan menu yang disediakan, yaitu: soto, rawon, gulai, nasi goreng, sate dan sop. Dari menu tersebut ternyata masing-masing anak tidak sama menu favoritnya.

_ Aris suka “rawon dan sop”, tetapi kali ini ia memesan rawon

_ Bari suka “soto, rawon dan gulai” , tetapi kali ini ia memesan gulai

_ Cecep suka “ sate dan nasi goreng” , namun makanan yang dipesannya adalah sate.

_ Fira memesan sate, karena ia memang hanya suka “sate” tersebut.

_ Darla anak baru jadi belum ada yang disukai, tetapi ia pesan nasi goreng

           

Dari peristiwa di atas Anda dapat membuat relasi antara dua himpunan, yaitu:

• Himpunan anak yang beranggotakan: Aris, Bari, Cecep, Darla dan Fira.

• Himpunan makanan yang beranggotakan: soto, rawon, gulai, nasi goreng, sate dan sop

Dalam hal ini kita dapat membuat dua macam relasi dengan aturan yang berbeda, yaitu: makanankesukaannya dan makanan pesanannya

· Relasi dengan aturan “makanan kesukaannya” sebagai berikut:Aris _ rawon ; Aris _ sop ; Bari _ soto ; Bari _ rawon ; Bari _ gulai ; Cecep _ sate ;Cecep _ nasi goreng ; Fira _ sate.

· Relasi dengan aturan “ makanan pesanannya” sebagai berikut:Aris _ rawon ; Bari _ gulai ; Cecep _ sate ; Darla _ nasi goreng _ ; Fira _ sate

  CARA MENYATAKAN RELASI ANTARA DUA HIMPUNAN

Pada pembahasan kali ini, diperkenalkan tiga cara menyatakan relasi, yaitu:

1. Dengan Himpunan Pasangan Berurutan

2. Dengan Diagram Panah

3. Dengan Diagram Cartesius

1. Dengan Himpunan Pasangan Berurutan

            Menyatakan relasi dengan himpunan pasangan berurutan dapat dilakukan dengan langkah-langkahsebagai berikut:

Langkah 1

Himpunan anak kita nyatakan sebagai himpunan A dan himpunan makanan yang disediakan olehrumah makan “Aneka Sari” kita nyatakan sebagai himpunan B.

Kita daftarkan masing-masing anggota himpunan A dan anggota himpunan B, yaitu:

A = {Aris , Bari , Cecep , Darla , Fira}

B = { soto, rawon, gulai, nasi goreng, sate, sop }

Langkah 2

Himpunan yang anggotanya semua pasangan berurutan (x , y) dinamakan himpunan pasangan berurutan

Kita pasangkan anggota himpunan A dan anggota himpunan B dengan aturan relasi: ”makanankesukaannya” dalam bentuk (x , y) dengan x € A dan y €B

c. Diagram Venn

Diagram Venn atau diagram set adalah diagram yang menunjukkan semua kemungkinan hubungan logika dan hipotesis di antara sekelompok (set/himpunan/grup) benda/objek. 

Contoh Soal 

Di antara 100 siswa, 32 orang suka PKn, 20 orang suka IPS, 45 orang suka IPA, 15 orang suka PKn dan IPA, 7 orang suka PKn dan IPS, 10 orang suka IPS dan IPA, 30 orang tidak suka satu pun di antara ketiga mata pelajaran tersebut. a) Hitung banyaknya siswa yang suka ketiga mata pelajaran tersebut; b) Hitung banyaknya siswa yang hanya suka satu dari ketiga matsa pelajaran tersebut; dan c) Gambarkan dengan Diagram Venn !

Penyelesaian:

Misalkan yang mengikuti ketiga mata pelajaran tersebut adalah x maka yang suka:

PKn dan IPA saja = 15-x

IPA dan IPS saja = 10-x

PKn  dan IPS saja = 7-x

PKn saja = 32 –(15-x)-(7-x)-x = 10+x

IPA saja = 45 –(15-x)-(10-x)-x = 20+x

IPS saja = 20 –(10-x)-(7-x)-x = 3+x

maka diagram vennya menjadi:

a) Unuk mencari jumlah siswa yang suka ketiga mata pelajaran tersebut, dengan mencari nilai x, caranya sebagai berikut:

100 – 30 = (3+x)+(20+x)+(10+x)+(7-x )+(10-x)+(15-x) + (x)

70 = 65 + x

x = 5

Jadi jumlah siswa yang suka ketiga mata pelajaran tersebut adalah 5 orang.

b) Unuk mencari jumlah siswa yang hanya suka satu dari ketiga mata pelajaran tersebut, caranya sebagai berikut:

PKn saja = 10+x = 10 + 5 = 15

IPA saja = 20+x = 20 + 5 = 25

IPS saja = 3+x = 3 + 5 = 8

Jumlah semua siswa yang hanya suka satu dari ketiga mata pelajaran = 15 + 25 + 8 = 48

Jadi, jumlah siswa yang hanya suka satu dari ketiga mata pelajaran tersebut adalah 48 orang.

c) Dengan memasukan nilai x maka diperoleh gambar Diagram Vennnya seperti gambar dibawah ini:

d. Operasi pada Himpunan

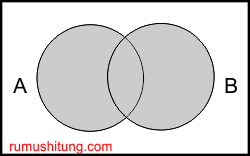
Gabungan (Union)
Gabungan dari A dengan B adalah A ∪ B = {x | x ∈ A atau x ∈ B}.

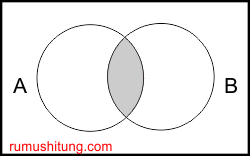
Irisan
Irisan dari A dan B adalah A ∩ B = {x | x ∈ A atau x ∈ B}.

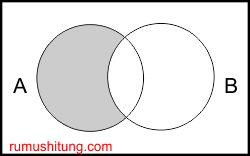
Selisih
Selisih dari A dengan B adalah A-B = {x | x ∈ A ataux ∉ B}

Jumlah
Jumlah dari A dengan B adalah A+B = {x | x ∈ A ∪ B dan x ∉ A ∩ B}

B. ALJABAR BOOLEAN 

Aljabar Boolen adalah himpunan yang memiliki dua operasi (+) dan (*) dan memenuhi aksioma berikut untuk setiap x, y, z ∊ B.

Teori dasar Aljabar Boolean terdiri dari: Elemen Identitas (x + 0 = x dan x . 1 = x), Komplemen (x + x’ = 1 dan x . x’ = 0), Tertutup (x + x =x; x + 1 = 1 dan x . x = x; x .0 = 0), Involusi ((x’)’ = x), Komutatif (x + y = y + x dan xy = yx), Asosiatif (x + (y + z) = (x + y) + z dan x(yz) = (xy)z), Distributif (x (y + z) = xy + xz dan x + (yz) = (x + y)(x + z)),De Morgan ( ( x + y)’ =x’y’ dan (xy)’ = x’ + y’), Absorpsi ( x + xy = x dan x ( x + y) = x ).

            Komplemen fungís merupakan statu fungsi yang memberikan nilai keluaran berkebalikan dengan fungsi awalnya. Sebagai conti suatu fungsi ( 0 menjadi 1 dan 1 menjadi 0). Sebagai contoh suatu fungsi K = (yz + x’y), Maka komplemennya adalah K’ = (y’ + z’)(x + y’).

            Fungsi Boolean-Bentuk Kanonikal terdiri dari dua terms, yaitu minterms dan maxterms, dimana setiap termsterdiri atas semua variabel yang ada.

Contoh:

K (x, y, z) = x’y’z + xy’z’

L (o, p, q) = (o + p’ + q)(o’ + p + q’)

            x’y’z , xy’z’ disebut minterms

            (o + p’ + q), (o’ + p + q’) disebut maxterms

            Funsi boolean bentuk standar terdiri dari 2 yaitu SOP (Sum of Product) dan POS (Product of Sum). SOP terdiri dari beberapa gerbang AND dan satu gerbang OR. Sebaliknya POS terdiri dari beberapa gerbang OR dan satu buah gerbang AND.

Penyederhanaan Fungsi Boolean

            Penyederhanaan sangat perlu dilakukan untuk membuat suatu fungsi menjadi lebih efisien dan mudah dipahami. Ada tiga cara penyederhanaan fungsi, yaitu: Menggunakan aturan Aljabar Boolean (secara matematis), Menggunakan Karnaugh map (K-map), dan menggunakan tabulasi (Quine McCluskey).

PRINSIP DUALITAS 

1.       Prinsip Dualitas

 Dalam sistem Aljabar Boolean dengan himpunan S dengan 0, 1 pada S serta operasi (+) dan (.). Ada himpunan S’ dengan mengganti 0 dengan 1, 1 dengan 0, (+) dengan (.), dan (.) dengan (+) berlaku semua aksioma Aljabar Boolean maka S’ disebut Dual dari S.

Teorema

Untuk setiap elemen a pada S berlaku :

1.       a + a = a dan a . a = a 2. a + 1 = 1 dan a . 0 = 0 3. a + a.b = a dan a . ( a + b ) = a 4. ( a . b )’ = a’ + b ‘ dan ( a + b )’ = a’ . b ‘ 5. 0’ = 1 dan 1’ = 0

Akan dibukti teorema 1 dan 2, pembuktian teorema yang lain dijadikan sebagai latihan dengan menggunakan aksioma yang berlaku pada sistem Aljabar Boolean

1 . a + a = a

Bukti :

a + a = ( a + a ) . 1 identitas (.)

= ( a + a ) . ( a + a’ ) komplemen

= a + ( a . a’ ) distributif

= a + 0 komplemen

= a identitas (+)

Terbukti

a . a = a

Bukti :

a . a = ( a . a ) + 0 identitas (+)

= ( a . a ) + ( a . a’ ) komplemen

= a . ( a + a’ ) distributif

= a . 1 komplemen

=a identitas (.)

Terbukti Maka a + a = a Dualnya adalah a . a =a

C. Gerbang Logika 

1. AND 

Gerbang AND akan berlogika 1 atau keluarannya akan berlogika 1 apabila semua masukan/inputannya berlogika 1, namun apabila semua atau salah satu masukannya berlogika 0 maka outputnya akan berlogika 0.

 

2. NAND

Gerbang NAND akan bernilai / outputnya akan berlogika 0 apabila semua inputannya bernilai 1 dan outpunya akan berlogika 1 apabila semua atau salah satu inputannya bernilai 0.